Lecture 14: Memory Hierarchy and Caching - Lectures on Computer Architecture

Click the thumbnail above to watch the video lecture on YouTube

By Dr. Isuru Nawinne

14.1 Introduction

This lecture marks a crucial transition from CPU-centric topics to memory systems, introducing cache memory as the elegant solution to the fundamental processor-memory speed gap. We begin with historical context, tracing how stored-program concept revolutionized computing, then explore the memory hierarchy that creates the illusion of large, fast memory through careful exploitation of temporal and spatial locality. The direct-mapped cache organization receives detailed treatment, establishing foundational concepts of blocks, tags, indices, and valid bits that underpin all cache designs. Understanding cache memory proves as essential as understanding processor architecture, as memory system performance often determines overall computer system speed in practice.

14.2 Lecture Introduction and Historical Context

14.2.1 Lecture Transition

Previous Topics:

CPU datapath and control (ARM, MIPS, pipelining)

New Focus:

Memory systems (equally important as CPU)

Motivation:

Memory plays as significant a role as CPU in modern computer architecture

14.2.2 Historical Background

Early Computing Machines (1940s)

Examples:

ENIAC (University of Pennsylvania)
Harvard Mark I (ASTC)

Characteristics:

Filled entire rooms
Built using vacuum tubes and electrical circuitry
Developed for war efforts (World War II)
Used for artillery planning, nuclear weapon calculations
No concept of software or memory as we know today

Programming Method:

Rewiring the entire machine for each algorithm
Engineers spent days/weeks reconfiguring machines
No stored program concept

14.2.3 Key Historical Figures

Alan Turing (1936)

British mathematician, brilliant mind
First conceived the stored program computer concept
Designed the Universal Turing Machine (hypothetical machine)
First notion of memory, programs stored in computers, data read/write operations
Later involved in World War II cryptography (Enigma Machine, "The Imitation Game")

John von Neumann (1940s)

Hungarian mathematician, regarded as "last of the brilliant mathematicians"
Prodigy: Solving calculus problems by age 8
Contributed across many fields
Got involved with EDVAC computer project
Implemented stored program concept based on Turing's ideas

14.2.4 First Stored Program Computers

EDVAC (1948)

Commissioned by U.S. Army
John von Neumann involved as consultant
Memory: Initially 1044 words, upgraded to 1024 words (power of 2)
First machine with stored program concept
Memory stored program electrically (not in wiring)
Engineers created the first "memory" device
First test programs: Nuclear weapon detonation calculations, hydrogen bomb calculations

Von Neumann Architecture

Key Concept:

Data AND instructions both in SAME memory
Access data and programs through SAME connection pathways
Unified memory for instructions and data
This concept became foundation of modern computers

EDSAC (Cambridge University)

Built about a year after EDVAC
First machine fully implementing Von Neumann architecture
Memory: 512 words of 18 bits each
Also built for war effort

Harvard Architecture (Contrasted)

Separate storages for instructions and data
Separate connections to instruction memory and data memory
Used in MIPS datapath design (separate instruction memory and data memory)

Modern Computers:

Use a MIX of both Von Neumann and Harvard architectures
Features from both types incorporated

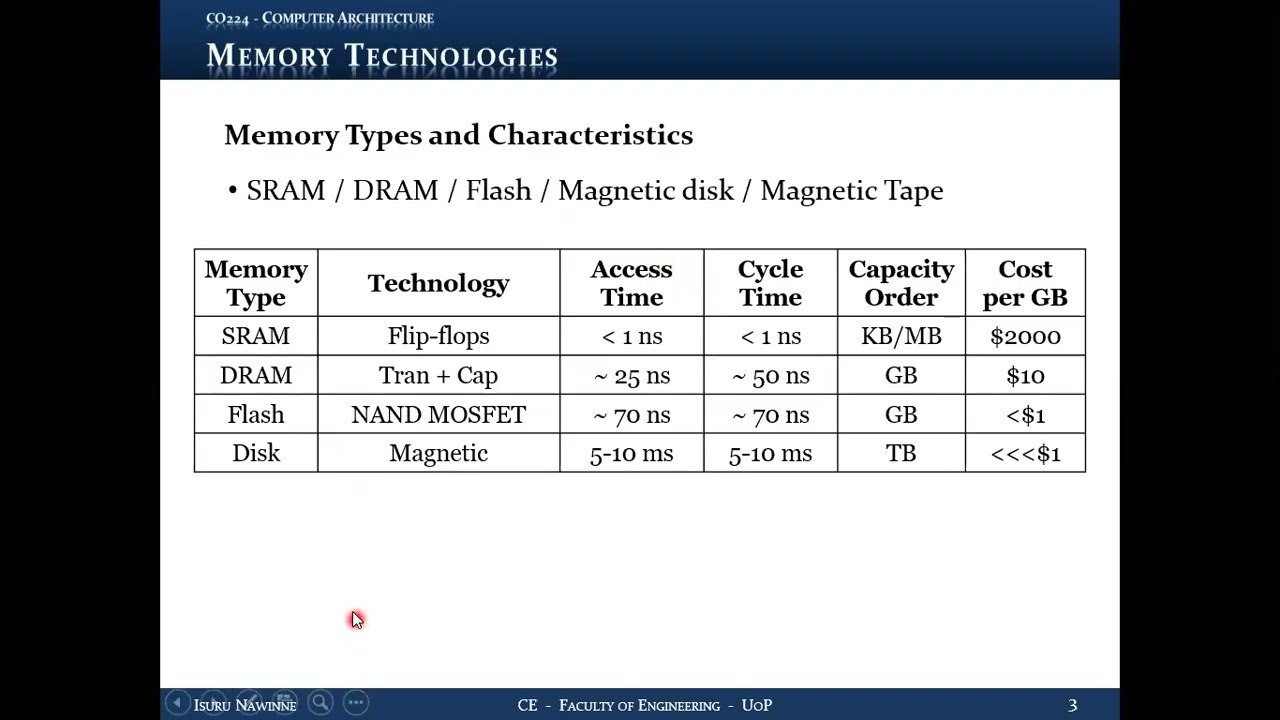
14.3 Memory Technologies: Types and Characteristics

14.3.1 Commonly Used Memory Technologies Today

SRAM (Static RAM)
DRAM (Dynamic RAM)
Flash Memory
Magnetic Disk
Magnetic Tape

14.3.2 SRAM (Static RAM)

Property	Value/Description
Technology	Built using flip-flops
Volatility	Volatile (loses content when power lost)
Access Time	Less than 1 nanosecond (< 1 ns)
Clock Frequency	More than 1 GHz
Cycle Time	Less than 1 nanosecond (< 1 ns)
Capacity	Kilobytes to Megabytes range
Cost	~$2000 per gigabyte (VERY EXPENSIVE)
Speed	Extremely fast
Usage	Cache memories (small amounts due to cost)

Note on Cycle Time:

Cycle time = minimum time between two consecutive memory accesses
Access time ≈ Cycle time for SRAM

14.3.3 DRAM (Dynamic RAM)

Property	Value/Description
Technology	Transistors + Capacitors
Volatility	Volatile (requires power AND periodic refresh)
Access Time	~25 nanoseconds (50 ns in some contexts)
Cycle Time	~50 nanoseconds (double the access time)
Capacity	Gigabytes (8 GB, 16 GB, or more)
Cost	~$10 per gigabyte
Usage	Main memory in computers

Key Characteristics:

Capacitor charge must be maintained
"Destructive read": Reading loses the charge, requires rewrite/refresh
Longer cycle time due to refresh requirement
After reading, must rewrite data to same cell
Significantly slower than SRAM (25-50 ns vs < 1 ns)

14.3.4 Flash Memory

Property	Value/Description
Technology	NAND MOSFET (NAND gate with two gates)
Volatility	Non-volatile (retains data without power)
Access Time	~70 nanoseconds
Cycle Time	~70 nanoseconds
Capacity	Gigabytes range
Cost	Less than $1 per gigabyte
Usage	Secondary storage (SSDs - Solid State Devices/Drives)

Limitation:

Limited read/write cycles
After several thousand cycles, memory cells may degrade
Integrity decreases, capacity effectively decreases
Slightly slower than DRAM, but non-volatile

14.3.5 Magnetic Disk

Property	Value/Description
Technology	Magnetic (mechanical device)
Access Time	5 to 10 milliseconds (MUCH slower than electronic memory!)
Cycle Time	Similar to access time (~5-10 ms)
Capacity	Several terabytes
Cost	Fraction of a dollar per gigabyte (very cheap)

Usage:

Previously: Main secondary storage
Currently: Being replaced by flash/SSDs for secondary storage
Now used primarily for tertiary storage, backups
Good for long-term data retention, low cost
Slowness acceptable for infrequent backup operations

Note: Average numbers; varies by data location on disk. Mechanical: spinning platters, moving read/write heads.

14.4 The Memory Performance Problem

14.4.1 The CPU-Memory Speed Gap

CPU Clock Cycle:

Modern CPUs: > 1 GHz clock frequency
Clock cycle: < 1 nanosecond (1 ns corresponds to 1 GHz)

Main Memory (DRAM):

Cycle time: ~50 nanoseconds
Time between starts of two consecutive memory accesses: 50 ns

14.4.2 The Problem

Speed Discrepancy:

CPU cycle: < 1 ns
Memory cycle: 50 ns
Memory is 50× SLOWER than CPU!

14.4.3 Impact on Pipelining

The Challenge:

In MIPS pipeline, MEM stage must finish in ONE clock cycle
Every pipeline stage must take same time
How can MEM stage complete in 1 ns when memory takes 50 ns?
Pipeline performance would be severely degraded

The Contradiction:

CPU expects 1 ns memory access
Actual DRAM takes 50 ns
"Something is not right" - how can this work?

14.5 Memory Hierarchy Concept

14.5.1 The Solution: Memory Hierarchy

Core Idea:

Trick the CPU into thinking memory is BOTH fast AND large
Desired characteristics:
- Fast access times (like SRAM: < 1 ns)
- Large capacity (like Disk: terabytes)
These characteristics don't exist in single technology
Solution: Implement memory as a HIERARCHY

14.5.2 Memory Hierarchy Structure

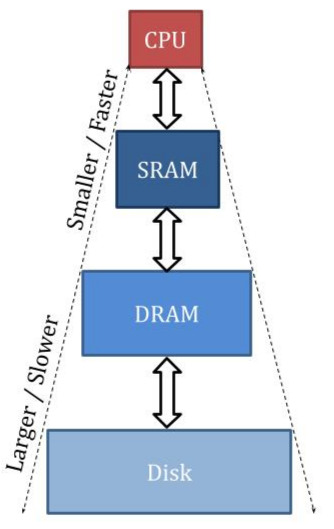
Memory Hierarchy with SRAM Cache, DRAM Main Memory, and Disk Storage

Level 1 (Top): SRAM (Cache)

Smallest capacity
Fastest speed
Closest to CPU physically

Level 2: DRAM (Main Memory)

Medium capacity
Medium speed

Level 3 (Bottom): Disk

Largest capacity
Slowest speed

14.5.3 Key Principles

1. CPU Access Restriction

CPU can ONLY access top level (SRAM cache)
CPU thinks cache is the actual memory
CPU cannot directly access DRAM or Disk

2. CPU's Perception

Experiences the SPEED of SRAM
Feels the CAPACITY of DRAM and Disk combined
Illusion: Memory is as fast as SRAM AND as big as lowest level

3. Data Organization

Upper levels contain SUBSET of data from lower levels
SRAM (few MB) contains subset of DRAM (several GB)
DRAM contains subset of Disk (several TB)
At any given time, each level holds only a fraction of lower level's data

4. Hierarchy Characteristics

Devices up the hierarchy: Smaller and faster
Devices down the hierarchy: Larger but slower

14.5.4 The Challenge

What if CPU asks for data NOT in the cache (top level)?

Need mechanism to copy data from lower levels
This leads to the concepts of hits, misses, and cache management

14.6 Analogy: Music Library

14.6.1 Understanding Memory Hierarchy Through Music

Three-Level Music System

1. Mobile Phone (analogous to SRAM/Cache):

Carries a subset of your favorite songs
Always with you
Listen to music directly from phone
Limited storage (like cache has limited capacity)

2. Computer Hard Disk (analogous to DRAM/Main Memory):

Main music collection stored here
Larger collection than phone
Not always accessible (not in pocket)
Copy songs from here to phone when needed

3. Internet (analogous to Disk/Mass Storage):

All songs available (massive storage)
Download/buy songs from here
Copy to computer, then to phone

14.6.2 Usage Scenarios

Scenario 1 (Hit)

Want to listen to a song
Song is already on phone
Just play it directly
Similar to cache hit: Data already in cache

Scenario 2 (Miss to Level 2)

Want to listen to a song
Song NOT on phone
Must go to computer and copy to phone
Then listen on phone
Similar to cache miss: Must fetch from main memory

Scenario 3 (Miss to Level 3)

Want to listen to a song
Song NOT on phone AND NOT on computer
Download from internet to computer
Copy to phone
Then listen
Similar to cache miss to disk: Must fetch from lowest level

14.6.3 Key Parallels

Always listen from phone (CPU always accesses cache)
Main collection in computer (main memory holds primary data)
All data available on internet (disk holds everything)
Copy operations when data not available at higher levels

14.7 Memory Hierarchy Terminology

14.7.1 Essential Terms for Memory Access

HIT

Definition: Requested data IS available at the accessed level

CPU requests data → Data found in cache
Like wanting to listen to song already on your phone
Can be served immediately from that level

MISS

Definition: Requested data is NOT available at the accessed level

CPU requests data → Data NOT found in cache
Like wanting to listen to song not on your phone
Must fetch from lower level in hierarchy

HIT RATE

Definition: Ratio/percentage of accesses that result in hits

Formula:

Hit Rate = (Number of Hits) / (Total Accesses)

Example: 100 accesses, 90 hits → Hit Rate = 90% or 0.9

Indicates how often data is found at the accessed level. Higher hit rate = better performance.

MISS RATE

Definition: Ratio/percentage of accesses that result in misses

Formula:

Miss Rate = (Number of Misses) / (Total Accesses)
Miss Rate = 1 - Hit Rate

Example: 100 accesses, 10 misses → Miss Rate = 10% or 0.1

Lower miss rate = better performance.

HIT LATENCY

Definition: Time taken to determine if access is a hit AND serve the data

Time to check if data is in cache and deliver it to CPU
For SRAM cache: < 1 nanosecond

Components:

Time to search cache
Time to verify data presence
Time to extract and send data to CPU

MISS PENALTY

Definition: EXTRA time required when access is a miss

Process:

Determine it's a miss (hit latency spent)
Go to next level (DRAM)
Find the data
Copy to cache
Put in appropriate place
Deliver to CPU

Key Points:

Total time on miss = Hit Latency + Miss Penalty
Miss penalty for DRAM access can be 100× hit latency
Very expensive in terms of time!

14.8 Performance Impact and Requirements

14.8.1 Average Memory Access Time

Formula:

Average Access Time = Hit Latency + (Miss Rate × Miss Penalty)

Explanation:

ALL accesses consume hit latency (must check cache)
Only misses consume additional miss penalty
Miss Rate determines portion of accesses incurring penalty

14.8.2 Example Analysis

Given:

Hit Latency (SRAM): < 1 nanosecond
Miss Penalty (DRAM access): ~100 nanoseconds (100× slower)
CPU clock cycle: < 1 nanosecond

For Pipeline to Work

MEM stage must complete in 1 clock cycle
Memory access must complete in < 1 ns most of the time

Required Hit Rate Calculation

If Hit Rate = 99.9% (Miss Rate = 0.1%):

Average Time = 1 ns + (0.001 × 100 ns)
             = 1 ns + 0.1 ns
             = 1.1 ns

Still close to 1 clock cycle!

If Hit Rate = 90% (Miss Rate = 10%):

Average Time = 1 ns + (0.10 × 100 ns)
             = 1 ns + 10 ns
             = 11 ns

Unacceptable! 11× slower than CPU clock!

14.8.3 Critical Requirement

Need VERY HIGH hit rate at cache level
Not just high, but VERY, VERY high
Target: 99.9% or better
Only 0.1% of accesses should go to memory

14.8.4 Performance Implications

With 99.9% Hit Rate

99.9% of time: CPU works fine, memory appears fast
0.1% of time: CPU must STALL, wait for data from DRAM
Stall is unavoidable for misses
Overall: CPU maintains illusion of fast, large memory

With Lower Hit Rate

More frequent stalls
Pipeline performance degrades significantly
Average memory access time increases
CPU slows down dramatically

Conclusion:

Must ensure VERY high hit rate at SRAM level
Memory hierarchy only works if locality principles hold
Like having most songs you want to listen to already on phone
Don't want to copy from computer frequently (time-consuming)

14.9 Principles of Locality

14.9.1 Foundation for Memory Hierarchy Success

Nature of Computer Programs:

Programs access only SMALL portion of entire address space at any given time
Address space: Entire memory range (address 0 to maximum address)
At any time window, program uses only small fraction of total data
True by nature of how programs are written, compiled, and executed
True for instruction sets like ARM, MIPS

14.9.2 Temporal Locality (Locality in Time)

Definition

"Recently accessed data are likely to be accessed again soon"

Explanation:

If you access memory address A at time T
High probability of accessing address A again at time T+ΔT (soon after)
Same data accessed multiple times in short time window
"Locality in time" - data clustered temporally

Common Examples in Programs

a) Loop Index Variables:

for (int i = 0; i < 100; i++) {
    // i is accessed every iteration
    // Same memory location for 'i' accessed repeatedly
}

b) Loop-Invariant Data:

for (int i = 0; i < n; i++) {
    result = result + array[i] * constant;
    // 'result' and 'constant' accessed every iteration
}

c) Function/Procedure Calls:

Local variables accessed multiple times during function execution
Same stack frame locations accessed repeatedly

d) Instructions:

Loop body instructions executed many times
Same instruction addresses accessed repeatedly

Music Analogy

If you listen to a song, you're likely to listen to it again soon
Sometimes listen to same song 10 times in a row
Want to replay favorite songs

Degree of Temporal Locality

Varies from program to program
But present in nearly ALL programs
Stronger in some (tight loops) than others

14.9.3 Spatial Locality (Locality in Space)

Definition

"Data located close to recently accessed data are likely to be accessed soon"

Explanation:

If you access memory address A at time T
High probability of accessing addresses A+1, A+2, A+3, ... soon after
Sequential or nearby addresses accessed together
"Locality in space" - data clustered spatially in memory

Common Examples in Programs

a) Array Traversal:

for (int i = 0; i < 100; i++) {
    sum += array[i];
    // Access array[0], then array[1], then array[2], ...
    // Sequential memory addresses
}

b) Sequential Instruction Execution:

Instructions stored sequentially in memory
PC increments: fetch instruction at PC, then PC+4, then PC+8, ...
Except for branches, mostly sequential

c) Data Structures:

struct Student {
    int id;
    char name[50];
    float gpa;
};
Student s;
// Accessing s.id, then s.name, then s.gpa
// Nearby memory locations

d) String Processing:

char str[] = "Hello";
for (int i = 0; str[i] != '\0'; i++) {
    // Access str[0], str[1], str[2], ...
    // Consecutive bytes in memory
}

Music Analogy

If you listen to song by artist X, likely to listen to another song by artist X
If you listen to song from album Y, likely to listen to next song in album Y
Related/nearby songs accessed together

Degree of Spatial Locality

Varies by data access patterns
Strong in array-based algorithms
Present in most structured programs

14.9.4 Universal Applicability

Both principles hold true for NEARLY ALL programs
Degree varies, but principles universally applicable
Foundation assumptions for cache design

14.10 Cache Memory Concept and Block-Based Operation

14.10.1 Cache Memory Overview

Purpose:

Memory device at top level of hierarchy
Based on two principles of locality
Decides what data to keep based on locality principles

14.10.2 Data Organization: BLOCKS

Key Concepts:

CPU requests individual WORDS from memory
Between cache and memory: Handle BLOCKS of data
Block = multiple consecutive words
Block size example: 8 bytes = 2 words (with 4-byte words)
Hidden from CPU (CPU still thinks in words)

14.10.3 Why Blocks? (Spatial Locality)

Instead of Words

Fetch single word CPU requested
Next access likely nearby address
Would require another fetch

Using Blocks

Fetch requested word AND nearby words together
Bring entire block (e.g., 8 consecutive bytes)
Subsequent accesses likely in same block (spatial locality)
Reduces future misses

Music Library Analogy

Want to listen to one song → Copy entire album to phone
Not just the single song you want right now
Because you'll likely want other songs from same album soon
Saves future copy operations

Block Benefits

Exploits spatial locality
Reduces miss rate
Amortizes fetch cost over multiple words
More efficient use of memory bandwidth

14.10.4 Cache Management Decisions

1. What to Keep in Cache

Based on BOTH locality principles
Recently accessed data (temporal locality)
Blocks containing nearby data (spatial locality)

2. What to Evict from Cache

Based on TEMPORAL locality
When cache full and need space for new block
Must throw out existing data

14.10.5 Eviction Strategy (Ideal)

Least Recently Used (LRU):

Throw out LEAST RECENTLY USED (LRU) data
If cache has 10 blocks, need to evict 1
Choose the block that was used longest time ago
Keep more recently used blocks
Temporal locality suggests LRU block least likely to be accessed soon

Example:

Cache has blocks A, B, C, D, E
Last access times: A(10 cycles ago), B(2 cycles ago), C(50 cycles ago), D(5 cycles ago), E(1 cycle ago)
Need to evict one block
Evict C (least recently used, 50 cycles ago)
Keep E, B, D, A (more recently used)

14.11 Memory Addressing: Bytes, Words, and Blocks

14.11.1 Byte Address

Definition: Address referring to individual byte in memory

Characteristics:

Each byte-sized location has unique address
Standard memory addressing
Address Space: With 32-bit address, can access 2³² individual bytes

Example Address:

Address: 00000000000000000000000000001010 (binary)
       = 10 (decimal)
Points to: Byte at memory location 10

Memory Structure:

Address 0:  [byte 0]
Address 1:  [byte 1]
Address 2:  [byte 2]
...
Address 10: [byte 10]  ← This byte addressed by example
...

14.11.2 Word Address

Definition: Address referring to a word (multiple bytes) in memory Typical Word Size: 4 bytes (32 bits)

Word Alignment

Words start at addresses that are multiples of 4
Word 0: Addresses 0, 1, 2, 3
Word 1: Addresses 4, 5, 6, 7
Word 2: Addresses 8, 9, 10, 11
Word 3: Addresses 12, 13, 14, 15

Word Address Format (32-bit)

[30-bit word identifier][2-bit byte offset]
                         └── Always "00" for word-aligned addresses

Example:

Address: ...00001000 (binary)
- Last 2 bits: 00 → Word-aligned
- Remaining bits: Identify which word
- This is address 8, start of word 2

Byte Within Word

Last 2 bits select byte within word:

00 → First byte (address 8)
01 → Second byte (address 9)
10 → Third byte (address 10)
11 → Fourth byte (address 11)

Key Points:

Word addresses are multiples of 4
Can divide by 4 without remainder
Last 2 bits = 00 for word addresses
NOT all addresses ending in 00 are word addresses, but word addresses end in 00
Only portion of address except last 2 bits identifies the word

14.11.3 Block Address

Definition: Address referring to a block (multiple words) in memory Example Block Size: 8 bytes = 2 words

Block Alignment

Blocks start at addresses that are multiples of 8
Block 0: Addresses 0-7
Block 1: Addresses 8-15
Block 2: Addresses 16-23
Block 3: Addresses 24-31

Block Address Format (32-bit)

[Block Identifier][3-bit offset]
                   └── Last 3 bits for 8-byte blocks

Example:

Address: 00000000000000000000000000101101 (binary)
       = 45 (decimal)

Block Address Portion:
- Ignore last 3 bits: 101 (offset part)
- Block address: 00000000000000000000000000101 (identifies block)
- This identifies the block containing address 45

Offset Within Block (3 bits for 8-byte blocks)

BYTE OFFSET (all 3 bits):

Used to identify individual BYTE within block:

000 → Byte 0
001 → Byte 1
...
111 → Byte 7

WORD OFFSET (most significant bit of offset):

Used to identify WORD within block (when block has 2 words):

0XX → First word (bytes 0-3)
1XX → Second word (bytes 4-7)
Only need 1 bit to select between 2 words

14.11.4 Address Components Summary

For address with 8-byte blocks, 4-byte words:

[Block Address][Word Offset][Byte in Word]
  ^              ^              ^
  |              |              └── 2 bits: Select byte within word
  |              └── 1 bit: Select word within block
  └── Remaining bits: Identify which block

Example Breakdown:

Address: ...00101101
- Last 2 bits (01): Byte offset within word → Byte 1 of word
- 3rd bit from right (1): Word offset → Second word of block
- Remaining bits (...00101): Block address → Block 5

All Bytes in Same Block:

Share same block address
Differ only in offset bits

Important Distinctions:

Byte address: Full 32 bits
Word address: Term refers to full address of word-aligned location
Block address: Term refers to portion of address identifying block (excluding offset)

14.12 The Cache Addressing Problem

14.12.1 Problem Statement

In Main Memory

Direct addressing: Address 10 → Direct access to location 10
Like array indexing: array[10] directly accesses index 10
Straightforward: Address uniquely identifies memory location
No search required: Hardware directly decodes address

In Cache

Cache is MUCH smaller than memory
Memory: Gigabytes (millions/billions of addresses)
Cache: Kilobytes or Megabytes (thousands/few million bytes)
Example: Memory has 1 million addresses, cache has only 8 slots

14.12.2 The Challenge

CPU generates address from full address space (e.g., address 10)
Cache has only 8 slots (indices 0-7)
Cannot directly use memory address as cache index
Address 10 doesn't directly map to cache location
How to find data in cache with memory address?

14.12.3 Initial Solution Idea: Store Addresses with Data

Approach:

Store memory address alongside data in cache
Each cache entry: [Address | Data]
When CPU requests address, search cache for matching address

Problems with This Approach:

1. Space Overhead:

Must store full address (e.g., 32 bits) with each data block
Significant storage overhead
Example: 32-bit address + 256-bit data block = ~13% overhead

2. Search Time:

Must search through ALL cache entries
Sequential or parallel search required
Example: 8 cache slots → Check all 8 tags
Time-consuming, degrades hit latency
Cannot directly access cache entry

14.12.4 Need for Better Solution

Requirements:

Require MAPPING between memory addresses and cache locations
Want DIRECT access (no search) if possible
Must be efficient in both space and time

Requirements for Practical Cache:

Fast access (< 1 ns hit latency)
Minimal storage overhead
Direct or near-direct cache indexing
Efficient tag comparison (if needed)

Solution Preview: Address Mapping Functions

Need function: Memory Address → Cache Location
Different mapping strategies possible
Simplest: Direct Mapping (discussed next)

14.13 Direct-Mapped Cache

14.13.1 Direct Mapping Concept

Definition:

Each memory address maps to EXACTLY ONE cache location
One-to-one deterministic mapping
No choice in cache placement

Mapping Rule:

Cache Index = Block Address MOD (Number of Blocks in Cache)

Formula:

Cache Index = (Block Address) mod (Cache Size in Blocks)

Example:

Cache has 8 blocks → Indices 0-7
Block address = 13
Cache index = 13 mod 8 = 5
Block 13 maps ONLY to cache index 5

14.13.2 Mathematical Properties

Mod Operation with Powers of 2

Cache sizes typically powers of 2 (1, 2, 4, 8, 16, 32, ...)
Mod by power of 2 = take least significant bits
Example: N mod 8 = N mod 2³ = last 3 bits of N

Hardware Implementation

No division circuit needed!
Simply extract least significant bits
Very fast, pure combinational logic

14.13.3 Direct Mapping Example

Given:

Block size: 8 bytes
Cache size: 8 blocks
Cache indices: 0, 1, 2, 3, 4, 5, 6, 7

Cache Structure (Initial View):

Index	Data Block
0	[64 bits]
1	[64 bits]
2	[64 bits]
3	[64 bits]
4	[64 bits]
5	[64 bits]
6	[64 bits]
7	[64 bits]

Example Addresses:

Address 1:

Binary: ...00000001[011]
        └─ Block address = 0
        └─ Offset = 3 bytes
Cache index = 0 mod 8 = 0
Maps to cache index 0

Address 2 (block address in focus):

Binary: ...00000101[000]
        └─ Block address = 5
        └─ Offset = 0
Cache index = 5 mod 8 = 5
Maps to cache index 5

14.13.4 Address Structure for Direct-Mapped Cache

[Tag][Index][Offset]
  ^     ^       ^
  |     |       └── Identifies byte/word within block
  |     └── Identifies cache location (index)
  └── Remaining bits to differentiate blocks mapping to same index

Bit Allocation (for 8-block cache, 8-byte blocks, 32-bit address)

Offset: 3 bits (for 8-byte blocks: 2³ = 8)
Index: 3 bits (for 8 cache blocks: 2³ = 8)
Tag: 26 bits (remaining: 32 - 3 - 3 = 26)

Index Bits

Least significant bits of block address
Directly select cache location
Number of bits = log₂(cache blocks)
8 blocks → 3 index bits
16 blocks → 4 index bits
32 blocks → 5 index bits

14.14 The Tag Problem in Direct-Mapped Cache

14.14.1 Conflict Issue

Multiple Blocks → Same Index:

Many memory blocks map to same cache index
Example: Blocks 5, 13, 21, 29, ... all map to index 5 (mod 8)
Only ONE can occupy cache index 5 at a time

Example Addresses Mapping to Index 5:

Address A:

Block address: ...00000101
Index bits (last 3): 101 → Index 5

Address B:

Block address: ...00001101
Index bits (last 3): 101 → Index 5

Both map to index 5, but different blocks!

14.14.2 The Problem

When CPU requests address with index 5
Is data at index 5 for Address A or Address B?
Need way to differentiate between conflicting blocks

14.14.3 Solution: TAG FIELD

Tag Definition:

Remaining bits of block address (excluding index and offset)
Stored WITH data in cache
Used to verify correct block is present

Tag = Block Address (excluding index bits)

Example Address Breakdown

Full Address:

[26-bit Tag][3-bit Index][3-bit Offset]

Address A

Binary representation:

00000000000000000000000000 101 000

Field	Bits (binary)	Decimal
Tag	00000000000000000000000000 (26 bits)	0
Index	101	5
Offset	000	0

Address B

Binary representation:

00000000000000000000000001 101 000

Field	Bits (binary)	Decimal
Tag	00000000000000000000000001 (26 bits)	1
Index	101	5
Offset	000	0

Both addresses map to cache index 5 but have different tag values (0 vs 1), so they refer to different memory blocks that conflict at the same cache index.

14.14.4 Cache Structure with Tags

Index	Valid	Tag	Data Block
0	V	Tag0	[64 bits]
1	V	Tag1	[64 bits]
2	V	Tag2	[64 bits]
3	V	Tag3	[64 bits]
4	V	Tag4	[64 bits]
5	V	Tag5	[64 bits]
6	V	Tag6	[64 bits]
7	V	Tag7	[64 bits]

Storage Requirements Per Cache Entry:

Tag: 26 bits (in this example)
Valid bit: 1 bit
Data: 64 bits (8 bytes)
Total: 91 bits per entry

Storage Overhead:

Overhead = (Tag + Valid) / Total
         = (26 + 1) / (26 + 1 + 64)
         = 27 / 91
         ≈ 30% overhead in this small example

Note on Overhead

Example uses VERY small cache (8 blocks)
Real caches are much larger (thousands of blocks)
Larger caches → More index bits
More index bits → Fewer tag bits
Overhead percentage decreases with larger caches

Example with Larger Cache:

1024 blocks (2¹⁰)
Index: 10 bits
Tag: 32 - 10 - 3 = 19 bits
Overhead: (19+1)/84 ≈ 24% (better)

14.14.5 Valid Bit

Purpose:

Indicates whether cache entry contains valid data
Prevents using uninitialized/stale data

Initial State:

At program start, cache is empty
All entries contain garbage/random values
All valid bits set to 0 (invalid)

After Data Loaded:

When block loaded into cache, valid bit set to 1
Indicates data is reliable

Uses Beyond Initialization:

Cache coherence (multi-processor systems)
Invalidating stale data
Handling context switches

14.15 Cache Read Access Operation

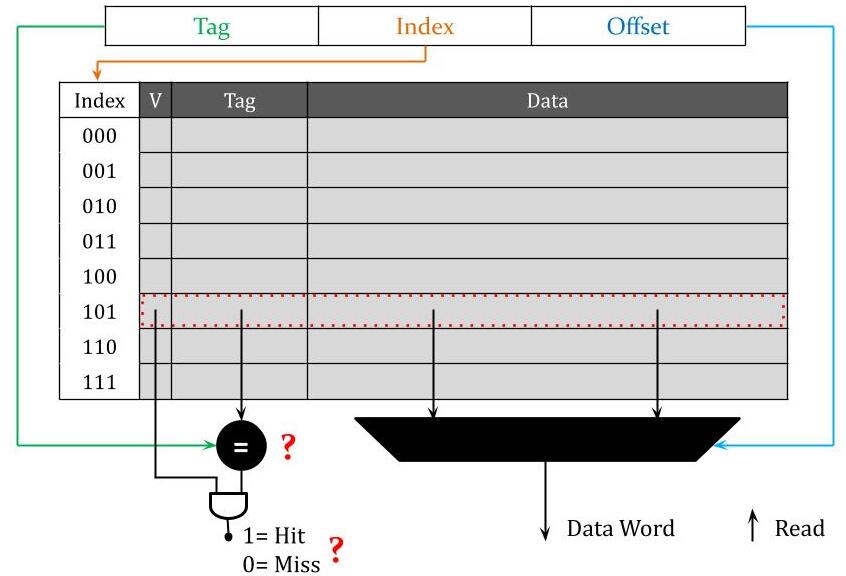
Direct-Mapped Cache Read Access Process

14.15.1 Read Access Process

CPU Provides:

Address (word or byte address)
Control Signal: Read/Write indicator (from control unit)

14.15.2 For Read Access

Step 1: ADDRESS BREAKDOWN

Process:

Receive address from CPU
Parse into three fields:

Tag bits
Index bits
Offset bits

Example Address (32-bit):

[26-bit Tag][3-bit Index][3-bit Offset]

Step 2: INDEXING THE CACHE

Extract index bits from address
Use index to directly access cache entry
Combinational logic routes to correct entry
Like array indexing: index 5 → entry 5
No search needed!
Fast: Pure combinational delay

Hardware:

Decoder circuit takes index bits
Selects one of N cache entries
Activates corresponding row

Step 3: TAG COMPARISON

Extract stored tag from selected cache entry
Extract tag bits from incoming address
Compare the two tags
Use comparator circuit

Comparator Circuit:

For each bit position: XNOR gate
XNOR outputs 1 if bits match, 0 if different
AND all XNOR outputs together
Final output: 1 if all bits match (tags equal), 0 otherwise

Example (4-bit tags):

Stored tag:   1 0 1 1
Address tag:  1 0 1 1
XNOR:         1 1 1 1  → AND = 1 (MATCH!)

Stored tag:   1 0 1 1
Address tag:  1 0 0 1
XNOR:         1 1 0 1  → AND = 0 (NO MATCH)

For N-bit tag:

N XNOR gates (parallel)
1 N-input AND gate
Very fast combinational circuit

Step 4: VALID BIT CHECK

Extract valid bit from selected cache entry
Check if entry is valid
Valid bit = 1 → Entry contains valid data
Valid bit = 0 → Entry is invalid (ignore)

Step 5: HIT/MISS DETERMINATION

Combine tag comparison and valid bit
Hit = (Tag Match) AND (Valid Bit = 1)
Miss = (Tag Mismatch) OR (Valid Bit = 0)

Logic Circuit:

Tag Match Output ─┐
                   AND ─→ Hit/Miss Signal
Valid Bit ────────┘

Output:

1 → HIT (data present and valid)
0 → MISS (data not present or invalid)

Hit Latency:

Time for steps 2-5, dominated by:

Indexing combinational delay
Tag comparator delay
Valid bit access
Typically < 1 nanosecond for SRAM

Step 6: DATA EXTRACTION (Parallel with Tag Check)

Can happen in PARALLEL with tag comparison
Extract entire data block from selected cache entry
Put data block on internal wires

Data Block:

Contains multiple words
Example: 8 bytes = 2 words (4 bytes each)

Step 7: WORD SELECTION (Using Offset)

CPU wants a single WORD, not entire block
Use offset bits to select correct word from block
Offset bits → Multiplexer select signal

Multiplexer (MUX):

Inputs: All words in the data block
Select: Word offset bits from address
Output: Selected word

Example (2 words per block):

Block contains: Word0 (bytes 0-3), Word1 (bytes 4-7)
Word offset = 0 → Select Word0
Word offset = 1 → Select Word1
Need 1-bit select for 2:1 MUX

Example (4 words per block):

Block contains: Word0, Word1, Word2, Word3
Word offset = 2 bits → Select among 4 words
Need 4:1 MUX

Timing:

Data extraction and word selection happen in parallel with tag check
Both combinational circuits
Similar delays
Can overlap operations

Step 8: DECISION BASED ON HIT/MISS

If HIT (signal = 1):

Selected word is correct data
Send word to CPU immediately
Access complete
Total time: Hit latency (< 1 ns)

If MISS (signal = 0):

Selected word is WRONG data (different block or invalid)
CANNOT send to CPU
Must fetch correct block from main memory (DRAM)
CPU must STALL (wait)
Cache controller takes over
Total time: Hit latency + Miss penalty

Miss Handling:

Will discuss in next lecture
Involves accessing main memory
Bringing block into cache
Potentially evicting old block
Then serving CPU request

14.16 Cache Circuit Components Summary

14.16.1 Key Circuit Elements

1. INDEXING CIRCUITRY

Input: Index bits from address
Function: Decoder to select cache entry
Output: Activates one cache row
Type: Combinational logic
Delay: Part of hit latency

2. TAG COMPARATOR

Input: Stored tag, Address tag
Function: Multi-bit equality check
Components:
- N XNOR gates (N = tag bit width)
- 1 N-input AND gate
Output: 1 if equal, 0 if not equal
Type: Combinational logic
Delay: Part of hit latency

3. VALID BIT CHECK

Input: Valid bit from cache entry
Function: Read and check validity
Output: 1 if valid, 0 if invalid
Type: Simple wire/buffer
Delay: Minimal

4. HIT/MISS LOGIC

Input: Tag match signal, Valid bit
Function: AND gate
Output: Hit/Miss signal
Type: Combinational logic
Delay: Single gate delay

5. DATA ARRAY ACCESS

Input: Index bits
Function: Read data block from cache
Output: Multi-word data block
Type: SRAM memory read
Delay: SRAM access time (parallel with tag check)

6. WORD SELECTOR (Multiplexer)

Input: Data block, Word offset bits
Function: Select one word from block
Output: Single word
Type: MUX (combinational)
Delay: MUX delay (parallel with tag check)

7. CONTROL LOGIC (Cache Controller)

Input: Hit/Miss signal, Read/Write control
Function: Decide next actions
Output: Control signals for CPU, memory
On Hit: Enable data to CPU
On Miss: Initiate memory fetch, stall CPU
Type: Sequential logic (state machine)

14.16.2 Hit Latency Components

Contributing Factors:

Indexing delay
Tag comparison delay
Valid bit check delay
Hit/Miss determination delay
Word selection delay (parallel)
Wire delays

Dominant Delays:

Indexing (decoder)
Tag comparator (XNOR + AND)
These determine critical path

Parallelism:

Tag check and data extraction happen simultaneously
Reduces total hit latency
Only one path delay counts (whichever is longer)

14.17 Next Lecture Preview

14.17.1 Topics to Cover

1. Cache Miss Handling

What happens after miss is determined?
How to fetch block from main memory?
Where to place new block in cache?
What to do if cache location occupied?

2. Cache Controller State Machine

Not just combinational logic
Sequential control needed for misses
Multiple clock cycles to handle miss
States: Idle, Compare Tags, Allocate, Write Back, etc.

3. Write Operations

Read operation covered this lecture
Write more complex: Must update cache AND memory
Write policies: Write-through, Write-back
Dirty bits for modified blocks

4. Replacement Policies

When cache full, which block to evict?
Least Recently Used (LRU)
Other policies: FIFO, Random, LFU

5. Performance Analysis

Calculate average access time
Impact of hit rate, miss penalty
Cache size vs. performance tradeoffs

6. Advanced Cache Concepts

Set-associative caches (beyond direct-mapped)
Multi-level caches (L1, L2, L3)
Fully associative caches

14.18 Key Takeaways and Summary

14.18.1 Historical Foundations

Early computers had no memory/software concept
Alan Turing conceived stored program computer (1936)
John von Neumann implemented it in EDVAC (1948)
Von Neumann architecture: Unified memory for instructions and data
Harvard architecture: Separate instruction and data memories

14.18.2 Memory Technologies Hierarchy

Technology	Speed	Size	Cost
SRAM	Fastest (< 1 ns)	Smallest (KB-MB)	Most expensive ($2000/GB)
DRAM	Medium (~50 ns)	Medium (GB)	Moderate ($10/GB)
Flash	Similar to DRAM	Gigabytes	Cheap (< $1/GB)
Disk	Slowest (5-10 ms)	Largest (TB)	Cheapest (cents/GB)

14.18.3 The Performance Problem

CPU cycle time: < 1 nanosecond
Main memory cycle time: ~50 nanoseconds
Memory 50× slower than CPU!
Pipeline requires memory access in 1 cycle
Cannot directly use DRAM for CPU memory accesses

14.18.4 Memory Hierarchy Solution

Multiple levels: SRAM (cache) → DRAM → Disk
CPU accesses only top level (cache)
Upper levels hold subsets of lower levels
Trick CPU: Fast as SRAM, large as Disk
Requires very high hit rate (> 99.9%) at cache level

14.18.5 Principles of Locality

1. Temporal Locality: Recently accessed data likely accessed again soon

Example: Loop variables, instructions in loops

2. Spatial Locality: Data near recently accessed data likely accessed soon

Example: Array elements, sequential instructions
Both principles present in virtually all programs
Foundation for cache effectiveness

14.18.6 Memory Addressing

Byte Address: Individual byte reference (full address)
Word Address: 4-byte word reference (last 2 bits = 00 for alignment)
Block Address: Multiple-word block reference (excludes offset bits)
Address structure: [Block Address][Offset]
Offset subdivides: [Word Offset][Byte in Word]

14.18.7 Cache Terminology

Hit: Data found in cache → Fast access (< 1 ns)
Miss: Data not in cache → Slow access (+ ~100 ns penalty)
Hit Rate: Fraction of accesses that hit (want > 99.9%)
Miss Rate: Fraction of accesses that miss (1 - Hit Rate)
Hit Latency: Time to determine hit and access data
Miss Penalty: EXTRA time to fetch from memory on miss

14.18.8 Cache Organization (Direct-Mapped)

Each memory block maps to exactly ONE cache location
Mapping: Cache Index = Block Address mod (Cache Size)
Address fields: [Tag][Index][Offset]
Index: Selects cache entry directly (no search!)
Tag: Differentiates blocks mapping to same index
Offset: Selects word/byte within block
Valid bit: Indicates if entry contains valid data

14.18.9 Direct-Mapped Cache Structure

Tag array: Stores tags for verification
Valid bit array: Validity indicators
Data array: Stores actual data blocks
Index not stored (implicit in position)

14.18.10 Cache Read Access Process

Extract index from address → Access cache entry
Extract tag from cache entry → Compare with address tag
Check valid bit from entry
Determine hit/miss: (Tag Match) AND (Valid)
In parallel: Extract data block, select word using offset
If HIT: Send word to CPU (done in < 1 ns)
If MISS: Must fetch from memory (will cover next lecture)

14.18.11 Critical Requirements

Hit latency must be < 1 CPU clock cycle
Hit rate must be very high (> 99.9%)
Only way to achieve: Exploit locality principles
Direct mapping enables fast indexing (no search)
Parallel tag check and data extraction minimize latency

14.18.12 Average Access Time Formula

Average Access Time = Hit Latency + (Miss Rate × Miss Penalty)

Must keep Miss Rate very low for performance
Even 1% miss rate catastrophic if penalty is 100×
Example: 1% miss rate → 1 + (0.01 × 100) = 2 ns average
Example: 0.1% miss rate → 1 + (0.001 × 100) = 1.1 ns average
Target: 99.9% or better hit rate

14.18.13 Pending Topics (Next Lectures)

Cache miss handling and memory fetch
Cache controller state machine
Write operations and write policies
Block replacement strategies (LRU, etc.)
Set-associative and fully associative caches
Multi-level cache hierarchies
Performance analysis and optimization

14.18.14 Music Library Analogy Summary

Phone (cache): Small, fast, always accessible
Computer (main memory): Larger, slower, main collection
Internet (disk): Huge, slowest, everything available
Listen from phone (CPU accesses cache)
Copy from computer when song not on phone (fetch on miss)
Download from internet when not on computer (fetch from disk)
Keep favorite songs on phone (exploit temporal locality)
Copy whole album at once (exploit spatial locality)

Key Takeaways

Stored-program concept revolutionized computing—programs stored in memory like data, eliminating manual reconfiguration for each algorithm.
Von Neumann architecture established fundamental computer organization—CPU, memory, and I/O with instructions and data sharing same memory.
Processor-memory speed gap creates performance bottleneck—CPU operates at nanosecond scale while main memory requires tens of nanoseconds.
Memory hierarchy provides illusion of large, fast memory—small fast cache near CPU, larger slower DRAM main memory, massive slow disk storage.
Temporal locality: Recently accessed data likely accessed again soon—programs exhibit loops, function calls, and repeated variable access patterns.
Spatial locality: Nearby data likely accessed soon—programs access arrays sequentially and instructions execute in order.
Cache exploits locality to achieve high hit rates—keeping frequently accessed data in fast storage dramatically improves average access time.
Cache organized in blocks, not individual words—exploiting spatial locality by fetching multiple words together.
Direct-mapped cache: Each memory block maps to exactly one cache location—simplest cache organization using modulo arithmetic for mapping.
Address breakdown: Tag + Index + Offset—index selects cache entry, tag identifies specific block, offset selects word within block.
Valid bit indicates cache entry contains meaningful data—essential for distinguishing real data from uninitialized entries at startup.
Cache hit occurs when requested data found in cache—CPU receives data in ~1 nanosecond, avoiding slow main memory access.
Cache miss requires main memory fetch—takes ~100 nanoseconds, replacing cache entry with new block from memory.
Hit rate determines cache effectiveness—even 1% miss rate significantly impacts average memory access time with 100× penalty.
Block size affects performance—larger blocks exploit spatial locality better but reduce total number of blocks, potentially increasing conflicts.
Cache size represents total data storage capacity—typical L1 caches 32-64 KB, L2 caches 256 KB-1 MB.
Tag comparison happens in parallel with data access—enabling fast hit detection and maintaining single-cycle cache access.
Music library analogy clarifies cache concept—phone (cache) holds favorites, computer (DRAM) has main collection, internet (disk) contains everything.
Cache transparent to programmer—software sees uniform memory, hardware manages cache automatically for best performance.
Memory hierarchy only works because programs exhibit locality—without temporal and spatial locality, caching would fail catastrophically.

Summary

The introduction to memory systems and cache memory reveals how the fundamental processor-memory speed gap—with CPUs operating 100× faster than main memory—drives sophisticated cache hierarchy designs that create the illusion of large, fast memory. Historical context from Alan Turing's theoretical foundations through Von Neumann's stored-program architecture establishes how modern computers execute instructions fetched from memory rather than requiring manual reconfiguration. The memory hierarchy concept, with small fast SRAM caches near the CPU, larger slower DRAM main memory, and massive disk storage, exploits two fundamental program properties: temporal locality (recently accessed data likely accessed again soon) and spatial locality (nearby data likely accessed soon). Cache memory, organized in blocks rather than individual words, dramatically improves average access time by maintaining frequently accessed data in fast storage, achieving hit rates often exceeding 95% in practice. Direct-mapped cache organization, the simplest mapping scheme, uses modulo arithmetic to assign each memory block to exactly one cache location, with address bits divided into tag (identifying specific block), index (selecting cache entry), and offset (choosing word within block). The valid bit distinguishes real cached data from uninitialized entries, essential at system startup when cache contains random values. Cache hits deliver data in approximately 1 nanosecond while misses require ~100 nanosecond main memory access, making even small miss rates significant—a 1% miss rate doubles average access time from 1 ns to 2 ns. The music library analogy effectively clarifies concepts: phone storage represents cache (small, fast, always accessible), computer storage represents main memory (larger, slower, main collection), and internet streaming represents disk (unlimited, very slow, backup). This cache transparency—programmer sees uniform memory while hardware automatically manages caching—enables software compatibility across different cache configurations. The critical insight remains that memory hierarchy effectiveness depends entirely on programs exhibiting locality; without these natural access patterns inherent to how we write code, caching would provide no benefit. Understanding cache fundamentals proves essential for both hardware designers optimizing cache architectures and software developers writing cache-friendly code that maximizes hit rates.

← Previous Lecture Next Lecture →